Hello again! I'm getting ready for an exam next year so let's relearn how to code merge sort in c. Unlike low level sorting like bubble sort and selection sort, merge sort is one of the fastest sorting algorithms for us to use, up there with the fastest one witch is quick sort.
Merge sort has the time complexity of O(n log(n)) that is way faster than bubble and selection that has O(n^2). Here's a table and a graph to better illustrate how the algorithms effect the performance:
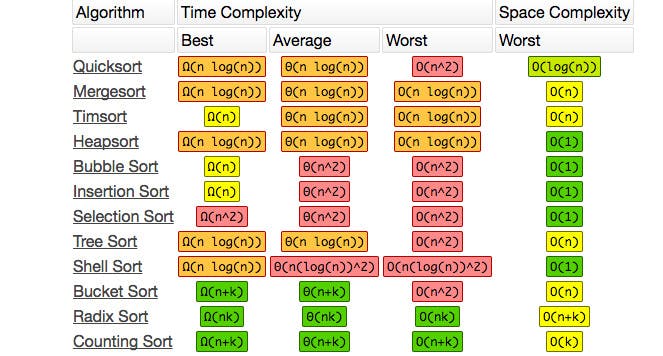
Source: https://www.linkedin.com/pulse/big-o-notation-time-complexity-algorithm-vikas-kumar/
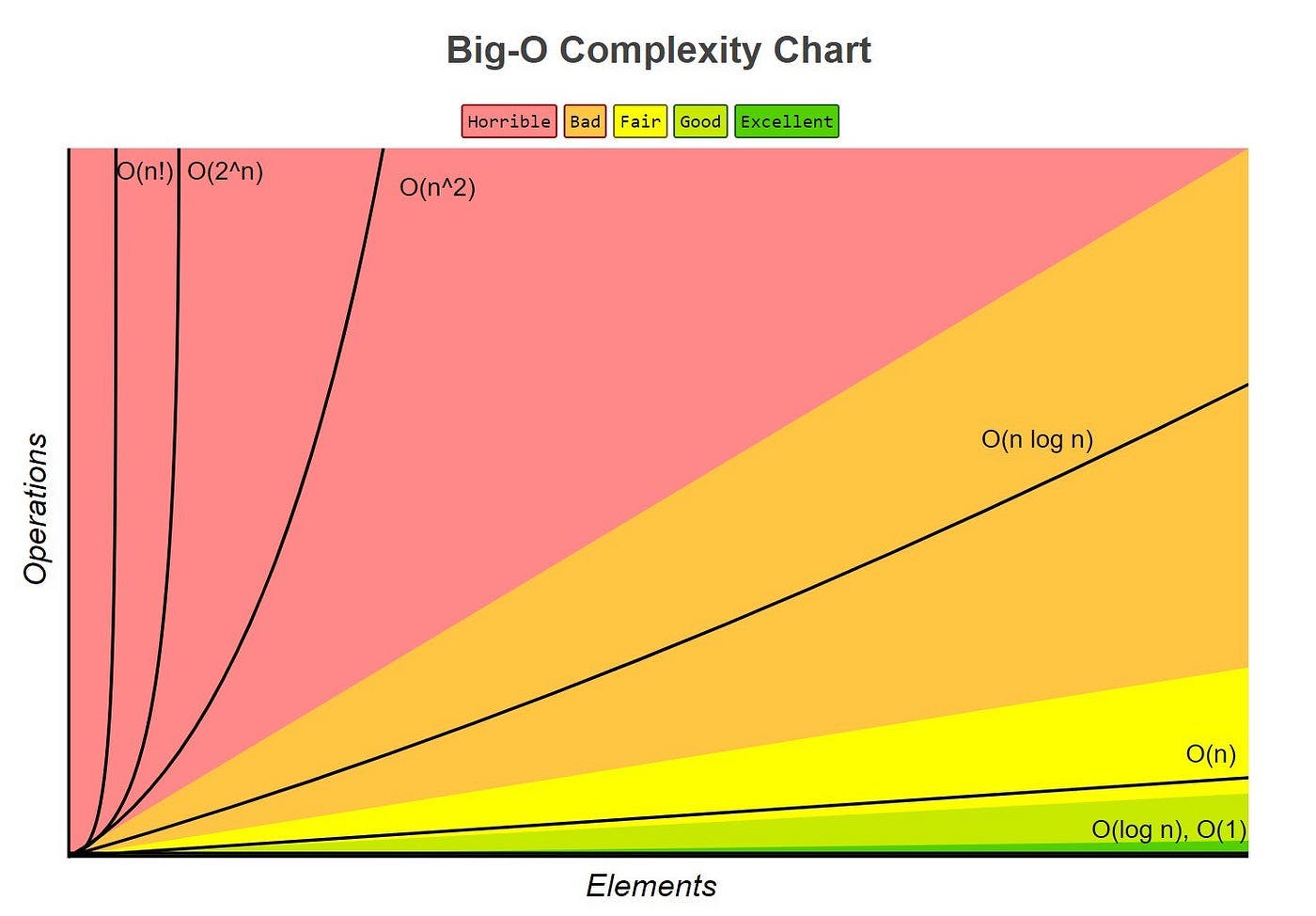
source: https://www.freecodecamp.org/news/big-o-cheat-sheet-time-complexity-chart/
The reason we will learn merge sort instead of quicksort is because it is easier to understand and code. Plus, closing in to the final exam in a few weeks, I feel like it is better to learn merge sort first before quicksort
How merge sort works, it separates the array into half splitting each time until there is only one. Merge sort works by merging two sorted arrays into one combined sorted array. And if you think about it, if you have an array that only has only one value, then it is already sorted. After that it combines the array again into sorted arrays each time merging into a bigger array until it has sorted the array.
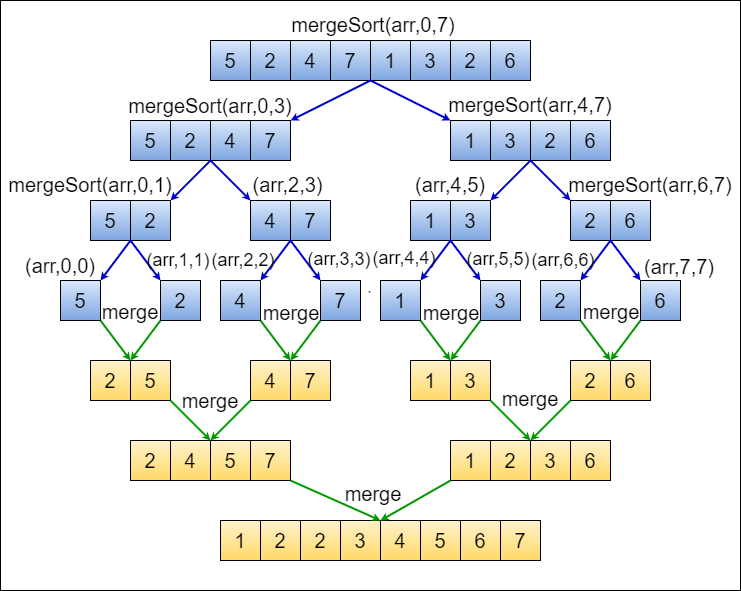
First when coding merge sort, you make two main functions below:
void Sorting_Merge(int array[], int left, int mid, int right){
}
void Recursion_Merge(int array[], int left, int right){
}
One is responsible for splitting the array over and over and the other function is responsible for sorting the splitted array. Be sure to make the variables like above, the variables left, mid, and right are index locations in the array.
Focusing on the Recursion_Merge function we make an if statement like this:
void Recursion_Merge(int array[], int left, int right){
if(left < right){
}
}
Think of it like if left is less than right then everything is still sane. If left is bigger than right than all hell broke lose and we need to stop it.
Inside of the if statement we need to calculate the midpoint index for it to be use by the Sorting_Merge and also splitting the array:
void Recursion_Merge(int array[], int left, int right){
if(left < right){
int mid = left + (right - left) / 2;
}
}
Like the name of the function, we split the array into two with recursion with the help of the mid integer we calculated:
void Recursion_Merge(int array[], int left, int right){
if(left < right){
int mid = left + (right - left) / 2;
Recursion_Merge(array, left, mid);
Recursion_Merge(array, mid+1, right);
}
}
Lastly we add the function Sorting_Merge after the recursion is done:
void Recursion_Merge(int array[], int left, int right){
if(left < right){
int mid = left + (right - left) / 2;
Recursion_Merge(array, left, mid);
Recursion_Merge(array, mid+1, right);
Sorting_Merge(array, left, mid, right);
}
}
Now that the recursion side is finished, we make the actual sorting part of the algorithm. Start by declaring a variable left and right length with this formula below:
void Sorting_Merge(int array[], int left, int mid, int right){
int left_length = mid - left + 1;
int right_length = right - mid;
}
Then, make a temporary array for left and right with the length of each left and right length we made:
void Sorting_Merge(int array[], int left, int mid, int right){
int left_length = mid - left + 1;
int right_length = right - mid;
int temp_left[left_length], temp_right[right_length];
}
Now we fill in the temporary arrays with the main array, with for loops:
void Sorting_Merge(int array[], int left, int mid, int right){
int left_length = mid - left + 1;
int right_length = right - mid;
int temp_left[left_length], temp_right[right_length];
for(int i = 0; i < left_length; i++)
temp_left[i] = array[left + i];
for(int i = 0; i < right_length; i++)
temp_right[i] = array[mid + i + 1];
}
we start filling the temp_left array from the left index of the main array plus i and we fill the right array from the mid index plus i and plus 1. The reason we increment it by 1 is because the temp_left array is already filling the mid point value.
Now comes the hard part of the algorithm, that is sorting the two arrays that we made into one sorted array. we first declare 3 variables named i, j, and k, and then we make a for loop like this:
void Sorting_Merge(int array[], int left, int mid, int right){
int left_length = mid - left + 1;
int right_length = right - mid;
int temp_left[left_length], temp_right[right_length];
for(int i = 0; i < left_length; i++)
temp_left[i] = array[left + i];
for(int i = 0; i < right_length; i++)
temp_right[i] = array[mid + i + 1];
int i,j,k; // as long as the left side is less than or equal than k
for(i = 0, j = 0, k = left; k <= right; k++){
}
}
Now pay attention! In the array we make a huge if statement like this:
int i,j,k; // as long as the left side is less than or equal than k
for(i = 0, j = 0, k = left; k <= right; k++){
if(i < left_length && (j >= right_length || temp_left[i] <= temp_right[j]))
array[k] = temp_left[i++];
else
array[k] = temp_right[j++];
}
/*
note that
array[k] = temp_left[i++];
is the same as
array[k] = temp_left[i];
i++;
*/
So basically, the variables i keeps track of temp_left, variable j keeps track of temp_right, and variable k keeps track of the merged array. k always incrementing so each time, it choses weather or not to choose the minimum value of temp_left or temp_right. example:
i
temp_left = {12,17}
j
temp_right = {13,14}
k
array = { , , , }
focus on (temp_left[i] <= temp_right[j]) witch means if the temp_left[i] is less than or equal to temp_right[j], then we fill the array[k] with temp_left[i], and increment i by 1 moving on to the next value and if not then we fill array[k] with temp_right[j] and increment j by 1.
The part (i < left_length) means if the index i is not out of bounds and the
(j >= right_length || ... ) means if the index j is almost out of bounds.
i
temp_left = {12,17}
j
temp_right = {13,14}
k
array = {12, , , }
It keeps doing this until it is sorted.
i
temp_left = {12,17}
j
temp_right = {13,14}
k
array = {12,13, , }
/////////////////////////////////////////////////////////
i
temp_left = {12,17}
j
temp_right = {13,14}
k
array = {12,13,14, }
/////////////////////////////////////////////////////////
i
temp_left = {12,17}
j
temp_right = {13,14}
k
array = {12,13,14,17}
And there you have it! a merge sort function for you to use!
void Sorting_Merge(int array[], int left, int mid, int right){
int left_length = mid - left + 1;
int right_length = right - mid;
int temp_left[left_length], temp_right[right_length];
for(int i = 0; i < left_length; i++)
temp_left[i] = array[left + i];
for(int i = 0; i < right_length; i++)
temp_right[i] = array[mid + i + 1];
int i,j,k; // as long as the left side is less than or equal than k
for(i = 0, j = 0, k = left; k <= right; k++){
if(i < left_length && (j >= right_length || temp_left[i] <= temp_right[j]))
array[k] = temp_left[i++];
else
array[k] = temp_right[j++];
}
}
void Recursion_Merge(int array[], int left, int right){
if(left < right){
int mid = left + (right - left) / 2;
Recursion_Merge(array, left, mid);
Recursion_Merge(array, mid+1, right);
Sorting_Merge(array, left, mid, right);
}
}
You can use it like this:
int main()
{
int arr[] = {5, 3, 0, 1, 2);
int len = sizeof(arr) / sizeof(arr[0]);
Recursion_Merge(arr, 0, len-1);
for(int i = 0; i < len; i++)
printf("%d ", arr[i]);
puts("");
}
We start the recursion from the left most index witch is 0 and the right most index witch is len -1.
You can practice sorting using this code i made. You can delete and remade merge sort and see your results. https://github.com/RasyaDevansyah/SortPractice
Merge sort is one of the fastest sorting algorithms, though quick sort is way faster and more memory efficient than merge sort because of not using so many temporary arrays, we still benefit from learning it. It's still surprises me how splitting array over and over again for it to be merge sorted is way faster than sorting it each 1 by 1. That's sums it up for me today, thankyou for reading and keep on learning.

